Research interests

Kicked Ising spin chain is an example of a model I like to study.

Broadly speaking, I am interested in the behaviour of many-body quantum systems away from equilibrium. I like to use the intuition and methods from quantum information. Below I provide some details about topics I am working on. For the current list of publications see my Google Scholar profile.

Novel solvable many-body systems and states:

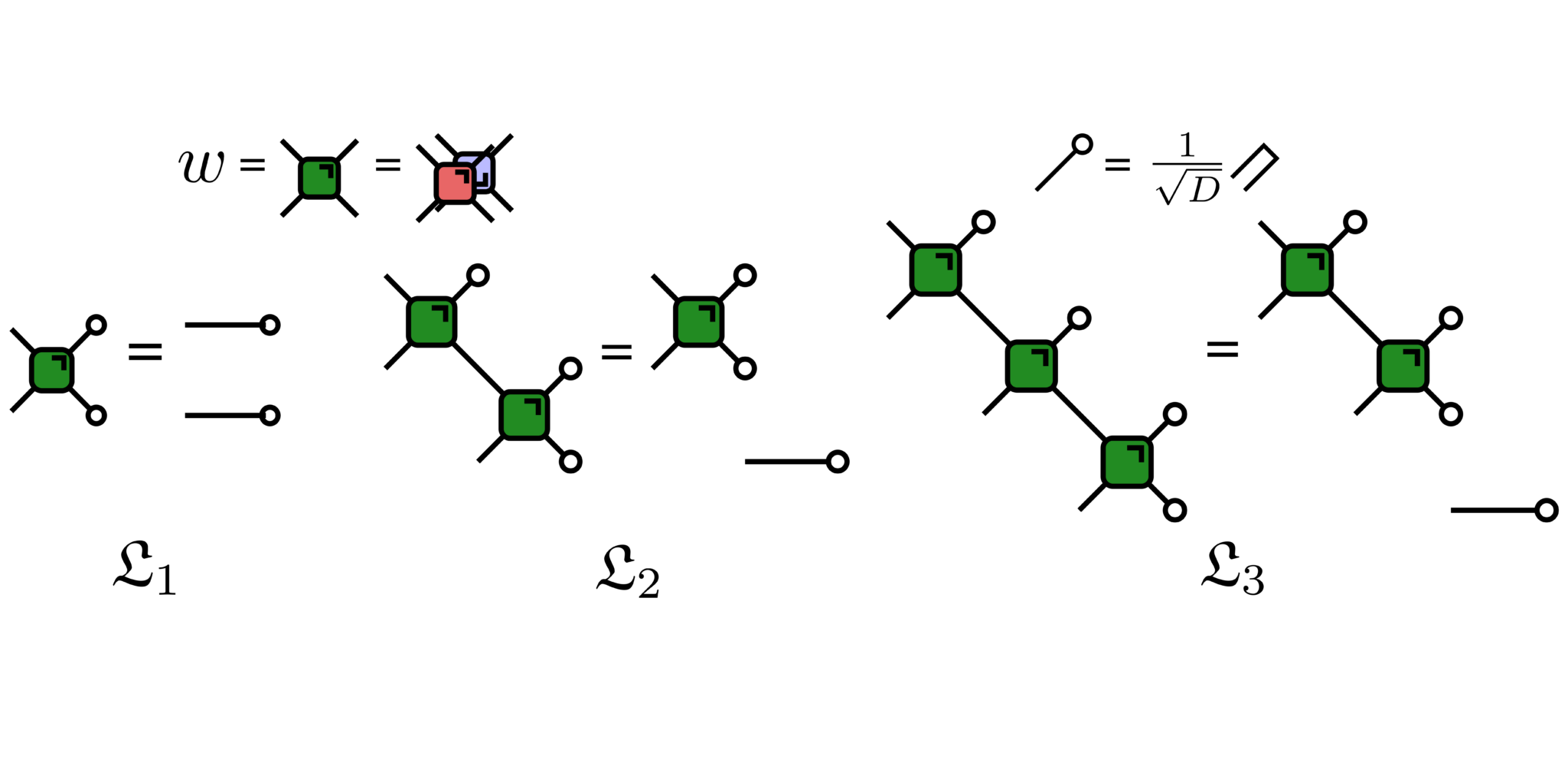Graphical conditions for hierarchical generalization of dual unitarity1.

During my PhD, we uncovered a novel class of solvable dynamics, called dual-unitary quantum circuits2. This class includes chaotic dynamics. Recently, I have been working on using similar ideas to uncover new solvable structures:

  • Generalizing this class to open systems: circuits of local quantum channels3.
  • Developing a hierarchy of solvable models4.
  • Investigating a solvable family of tensor network states1.

I also numerically and analytically investigate models exhibiting localization, such as the quantum east model5 and strong localization6,7.

A relevant online talk from QChaos2020 - Quantum chaos online seminar series: Solvable Chaotic Many-Body Quantum Systems

Many-body quantum chaos:

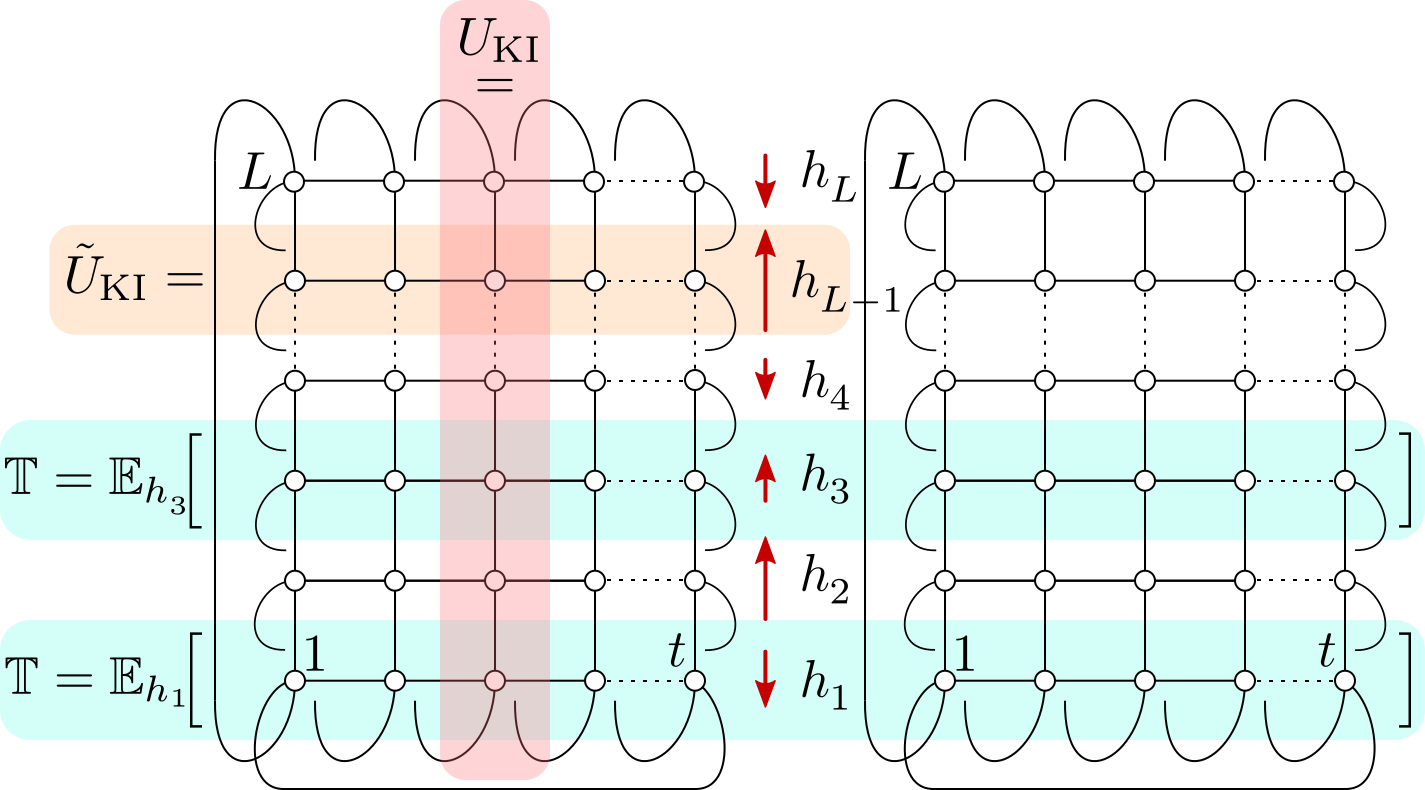Expression for the spectral form factor of kicked Ising spin chain8.

I am interested in the notions of quantum chaos, and their connections with the generation of complexity, ergodicity and thermalization.

The most established signature of quantum chaos is that spectral fluctuations match random matrix theory. For analytical treatment, a convenient representation of spectral data is spectral form factor (SFF). Using it, me and my collaborators provided some of the first exact results on quantum chaos in many-body systems7–11. For instance, in11 we proved that dual-unitary models are chaotic 1.

Another interesting indicator of chaos is the local operator entanglement entropy. It is the entanglement of vectorized Heisenberg-evolved local operators, and it measures their complexity. It signals how hard it is to express this operator using tensor networks. It grows linearly for chaotic models and at most logarithmic for free and integrable models. We investigated it for dual-unitary models12, circuits with solitons13, and its connection with out-of-time-correlators (OTOCs)14.

Dynamics of many-body quantum systems:

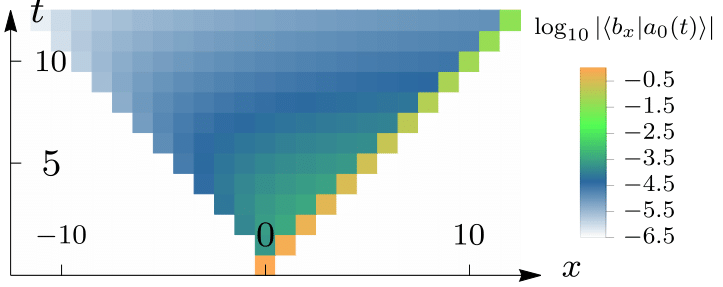Analitically accesible correlation functions in perturbed dual-unitary models15.

I use the novel solvable circuits, to gain insight into the dynamics of chaotic (generic) systems. For that, I use correlation functions2,15 , generation of entanglement entropy16,17, local operator entanglement generation12–14, magic generation18, and OTOCSs17.

References

1 X.-H. Yu, J.I. Cirac, P. Kos*, and G. Styliaris*, “Dual-isometric projected entangled pair states,” arXiv:2404.16783, (2024).

2 B. Bertini, P. Kos, and T. Prosen, “Exact Correlation Functions for Dual-Unitary Lattice Models in $1+1$ Dimensions,” Phys. Rev. Lett. 123, 210601 (2019).

3 P. Kos*, and G. Styliaris*, “Circuits of space and time quantum channels,” Quantum 7, 1020 (2023).

4 X.-H. Yu, Z. Wang, and P. Kos, “Hierarchical generalization of dual unitarity,” Quantum 8, 1260 (2024).

5 B. Bertini, P. Kos, and T. Prosen, “Localized dynamics in the floquet quantum east model,” Phys. Rev. Lett. 132, 080401 (2024).

6 B. Bertini, P. Kos, and T. Prosen, “Exact spectral statistics in strongly localized circuits,” Phys. Rev. B 105, 165142 (2022).

7 P. Kos, T. Prosen, and B. Bertini, “Thermalization dynamics and spectral statistics of extended systems with thermalizing boundaries,” Phys. Rev. B 104, 214303 (2021).

8 B. Bertini, P. Kos, and T. Prosen, “Exact Spectral Form Factor in a Minimal Model of Many-Body Quantum Chaos,” Phys. Rev. Lett. 121, 264101 (2018).

9 P. Kos, M. Ljubotina, and T. Prosen, “Many-Body Quantum Chaos: Analytic Connection to Random Matrix Theory,” Phys. Rev. X 8, 021062 (2018).

10 P. Kos, B. Bertini, and T. Prosen, “Chaos and ergodicity in extended quantum systems with noisy driving,” Phys. Rev. Lett. 126, 190601 (2021).

11 B. Bertini, P. Kos, and T. Prosen, “Random matrix spectral form factor of dual-unitary quantum circuits,” Communications in Mathematical Physics, (2021).

12 B. Bertini, P. Kos, and T. Prosen, “Operator Entanglement in Local Quantum Circuits I: Chaotic Dual-Unitary Circuits,” SciPost Phys. 8, 67 (2020).

13 B. Bertini, P. Kos, and T. Prosen, “Operator Entanglement in Local Quantum Circuits II: Solitons in Chains of Qubits,” SciPost Phys. 8, 68 (2020).

14 N. Dowling, P. Kos, and K. Modi, “Scrambling is necessary but not sufficient for chaos,” Phys. Rev. Lett. 131, 180403 (2023).

15 P. Kos, B. Bertini, and T. Prosen, “Correlations in perturbed dual-unitary circuits: Efficient path-integral formula,” Phys. Rev. X 11(1), 011022 (2021).

16 B. Bertini, P. Kos, and T. Prosen, “Entanglement Spreading in a Minimal Model of Maximal Many-Body Quantum Chaos,” Phys. Rev. X 9, 021033 (2019).

17 A. Foligno, P. Kos, and B. Bertini, “Quantum information spreading in generalised dual-unitary circuits,” arXiv:2312.02940, (2023).

18 J.A. Montañà López, and P. Kos, “Exact solution of long-range stabilizer rényi entropy in the dual-unitary XXZ model,” arXiv:2405.04448, (2024).

  1. When disorder can be taken to zero after the thermodynamic limit ↩︎